More examples

• n-queens
• Sudoku
• Survo puzzle

n-queens

The n-queens problem consists in placing n queens on an n×n chess board, in a such manner that no two queens attack each other.

A solution for then 8-queens problem

Maybe the simpliest way to model this problem consists in finding where to put each queen, i.e finding a couple of integers (x, y) representing coordinates for each queen.
Using this approach, here is a generic function that solves the n-queens problem :

template<int N>
void queens()
{
    typedef SInt<1, N> Coord;                           // Defines Coord as a Specialized Int type.
    typedef Tuple<Coord, Coord> Coords;                 // Each queen is to be assigned a Coords.

    List<Coords> queens(N);                             // Declares N queens.

    for (int i = 0 ; i < N ; ++i)
    for (int j = i+1 ; j < N ; ++j)
    {
        queens[i].first() != queens[j].first();         // No two queens share the same column.

        queens[i].second() != queens[j].second();       // No two queens share the same row.

        abs(queens[i].first() - queens[j].first()) !=   // No two queens share the same diagonal.
        abs(queens[i].second() - queens[j].second());
    }

    cout << solutions(queens);                          // Prints all the solutions.
}

Sudoku

As Wikipedia states, the objective of this famous game is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9.

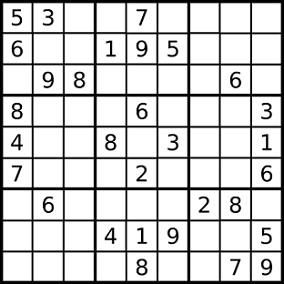
A Sudoku taken from Wikipedia

Can you think of a ten line program that solves any Sudoku (apart of the input/output stages) ?
Using the EasyCP Library, this is quite an easy job :

typedef SList<SList<SInt<1, 9>, 9>, 9> SudokuBoard;


istream & operator>>(istream & in, SudokuBoard & Board)
{
    char c;

    for (int y = 0 ; y < 9 ; ++y)
    for (int x = 0 ; x < 9 ; ++x)
    {
        in >> c;
        if (c != '.')
            Board[y][x] == int(c - '0');
    }

    return in;
}


void solve_sudoku(const string & input)
{
    istringstream iss(input);
    SudokuBoard Board;                          // Declares the board.
    iss >> Board;                               // Constrains the Board so as to satisfy the 'input' pattern.

    for (int ay = 0 ; ay < 9 ; ++ay)            // For each square a(ax, ay),
    for (int ax = 0 ; ax < 9 ; ++ax)
        for (int by = ay ; by < 9 ; ++by)       //    For each square b(bx, by) coming "after" a,
        for (int bx = (by == ay ? ax+1 : 0) ; bx < 9 ; ++bx)
            if (ax == bx || ay == by || (ax/3 == bx/3 && ay/3 == by/3))
                Board[ay][ax] != Board[by][bx]; //        a != b if they share the same column, row, or 3×3-square.

    cout << to_string(solutions(Board));        // Prints all the solutions.
}


void sudoku()
{
    solve_sudoku(
        "53..7...."
        "6..195..."
        ".98....6."
        "8...6...3"
        "4..8.3..1"
        "7...2...6"
        ".6....28."
        "...419..5"
        "....8..79"
    );
}

Survo puzzle

In a Survo puzzle the task is to fill an m x n table by integers 1,2,...,m*n so that each of these numbers appears only once and their row and column sums are equal to integers given on the bottom and the right side of the table.
(see Wikipedia's page for further explanation)

Wikipedia's first exemple of Survo puzzle

This problem is very like the Sudoku one, and so is our way to solve it.
This time, however, we decide to put the constraints directly in the function that read the data from a c++ stream.

template<class TList>
std::istream & operator>>(istream & in, TList & Grid)
{
    const int nb_lines = Grid.static_size();
    const int nb_columns = Grid[0].static_size();

    List<SInt<0, 0> > TotalColumns(nb_columns);

    for (int y = 0 ; y < nb_lines ; ++y)
    {
        for (int x = 0 ; x < nb_columns ; ++x)
        {
            int n;
            in >> n;
            if (n != 0) Grid[y][x] == n;

            TotalColumns[x] += Grid[y][x];
        }

        int totalCurLine;
        in >> totalCurLine;

        sum(Grid[y]) == totalCurLine;
    }

    for (int x = 0 ; x < nb_columns ; ++x)
    {
        int totalCurColumn;
        in >> totalCurColumn;

        TotalColumns[x] == totalCurColumn;
    }

    all_diff(flatten(Grid));

    return in;
}

This model demonstrates two important features of the EasyCP library :

• The use of functions that operate on Lists (sum, all_diff, flatten).
• The use of a common idiom of imperative programming, to "accumulate" a sum in a cp-variable.
  EasyCP allows you to mix imperative and constraint programming styles freely. If you are not comfortable with both styles, you may prefer not use such a feature.
  For further explanation, see the section Value semantics in more_on_variables() in advanced_features() in src/Demo/demo.cpp

void survo_puzzle()
{
    cout << endl << "solving the a Survo puzzle..." << endl;

    const int nb_lines = 3;
    const int nb_columns = 4;

    istringstream input(
        "0  6   0   0   30 \n"
        "8  0   0   0   18 \n"
        "0  0   3   0   30 \n"
        "27 16  10  25     \n"
        );

    typedef SList<SList<SInt<1, nb_columns*nb_lines>, nb_columns>, nb_lines> Grid_t;
    Grid_t Grid;                            // Declares the Grid.

    input >> Grid;                          // Loads the data into the Grid.

    // Use this syntax to read the data directly from the console :
    // cin >> Grid;

    // Use this syntax to read the data from a file :
    // ifstream file("data.txt");
    // file >> Grid;

    SolSet<Grid_t> S(Grid);

    // pretty print :

    int i = 0;
    for (SolSet<Grid_t>::iterator iSol = S.begin() ; iSol != S.end() ; ++iSol)
    {
        cout << "solution #" << ++i << " :" << endl;
        for (int y = 0 ; y < iSol->static_size() ; ++y)
            cout << iSol->at(y) << endl;    // prints a line at a time
    }
    cout << endl;

    // alternatively, this prints one solution per line :

    // cout << to_string(S);
}